Objectifs de la séance

  • Visualisation de données
    • Boîte à moustaches
  • Analyse de données
    • Construire un test de conformité à une valeur
    • Construire un test de comparaison de moyennes
    • Adapter la règle de décision pour un test unilatéral

Exercices

Recueil des données

A l’oeil, sans l’aide d’outil (rapporteur, règle ou compas) et indépendamment de vos voisins, évaluer l’angle (en degrés) entre AB et AC (selon votre groupe, celui de la figure 1 ou de la figure 2).

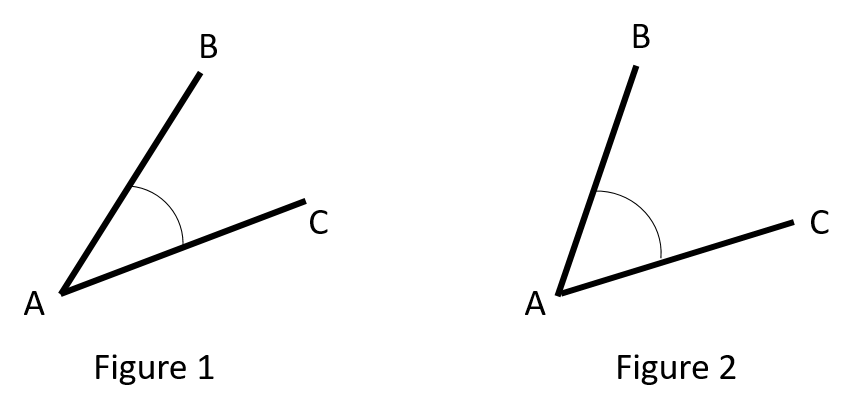
Evaluation de l’angle entre AB et AC

Une fois toutes les données recueillies, considérons deux groupes : les évaluations faites par les garçons et les évaluations faites par les filles. On suppose que la mesure d’un angle suit une loi normale d’espérance \(\mu_{1}\) et de variance \(\sigma^2\) lorsqu’elle est évaluée par des garçons et une loi normale d’espérance \(\mu_{2}\) et de variance \(\sigma^2\) lorsqu’elle est évaluée par des filles.

Importation du jeu de données

  • Saisir les données et les sauvegarder dans un fichier angle.csv.

  • Importer le jeu de données angle.csv dans un objet nommé don_Angle en utilisant un script TD5_script.R que vous aurez créé dans votre répertoire de projet.

Visualisation des données

  • Visualiser les données pour avoir une idée de la distribution des angles pour les garçons, et pour les filles. Calculer quelques statistiques par sexe.

Test statistique

Mise en place de l’analyse statistique

On cherche dans un premier temps à savoir si, en moyenne, les filles ont une évaluation non biaisée de l’angle.

  • Exprimer la problématique ci-dessus sous la forme d’un test d’hypothèses.

  • Dans cette problématique de test, quel est l’échantillon et quelle est la population ?

  • A l’aide des données recueillies, mettre en oeuvre le test avec un niveau de confiance de 95 % (i.e. un seuil de 5 % pour l’erreur de type I). Vous utiliserez la fonction t.test et adapterez la ligne de code suivante en ne sélectionnant que les filles (n’hésitez pas à voir l’aide de la fonction en faisant help('t.test')). La fonction t.test permet à la fois de construire le test d’égalité de la moyenne à une valeur et de construire un intervalle de confiance.

don_Angle  %>% select(Angle) %>% t.test(mu=angle_ref)

  • Pour les garçons, tester si, en moyenne, ils évaluent justement ou s’ils sous-estiment l’angle (préciser \(H_0\) et \(H_1\) avant de construire le test sous R).

  • On souhaite maintenant tester l’égalité des moyennes entre garçons et filles. Préciser l’hypothèse \(H_0\) et l’hypothèse \(H_1\). La fonction t.test permet également de construire un test d’égalité de 2 moyennes.

Et en utilisant un modèle d’analyse de variance

On propose d’utiliser les fonctions lm et anova de la façon suivante. Expliciter ce que font chaque ligne de code et à quoi correspondent les résultats obtenus par rapport aux résultats précédents.

mod <- lm(Angle~Sexe, data = don_Angle)
m0 <- lm(Angle~1, data = don_Angle)

summary(mod)
anova(m0, mod)

Conclusion de l’étude

  • Quel pourrait être l’intérêt d’utiliser un modèle et les fonctions lm et anova plutôt que de construire un test d’égalité de 2 moyennes avec la fonction t.test ? Et quel est l’intérêt de la fonction t.test ?

Le vocabulaire de la séance

Commandes R

  • as.factor
  • group_by
  • t.test
  • lm
  • anova

Environnement R

Statistique

  • Test d’égalité de 2 moyennes
  • Test de conformité
  • Test unilatéral