TD3 : Tester l’existence d’un effet groupe

Objectifs de la séance

Manipulation de données
- Grouper les données par modalité d’un facteur
- Effectuer des calculs par modalité du facteur
Visualisation de données
- Boîte à moustaches
Analyse de données
- Démarche statistique
- Reconnaître le contexte d’une analyse de la variance
- Ecrire le modèle correspondant
- Mettre en oeuvre le test du modèle complet

Exercices

Le problème qui suit est inspiré d’un stage de fin d’études réalisé par une étudiante de la spécialisation Science des données du cursus d’ingénieur agro-alimentaire d’Agrocampus.

Un groupe industriel commercialisant du café souhaite comparer les cafés provenant de différents lieux de production à partir de leur profil de composition physico-chimique, dont une des composantes importantes est le taux de matière sèche (DM). Pour cela, il s’appuie sur des données contenant le lieu de production, codé par un entier allant de 1 à 7, de 240 mesures de café disponible sur l’onglet Scripts et données de la page d’accueil du module.

Description des données sur la qualité du café

Importation des données

Importer le fichier de données cafe_DM.csv disponible sur la page des jeux de données dans un objet nommé cafe en utilisant un script TD3_script.R que vous aurez créé dans votre répertoire de projet.
Quels sont les noms des variables de ce tableau de données ?
La nature de chacune de ces variables, telle que déclarée dans R, correspond-elle à votre appréciation personnelle ?

R traite la variable Localisation, un entier compris entre 1 et 7, comme une variable quantitative. Il faut indiquer à R que cette variable est en fait une variable qualitative, un facteur :

cafe <- cafe %>% 
  mutate(Localisation = as.factor(Localisation))

Après cette transformation, la nature de chacune de ces variables correspond-elle finalement à votre appréciation personnelle ?

Visualisation des données

Construire maintenant une boîte à moustaches des taux de matière sèche pour chaque site de production des cafés.

Calcul de statistiques descriptives

La commande suivante permet de calculer la moyenne de matière sèche pour chaque site de production de café :

cafe %>% 
  group_by(Localisation) %>% 
  summarise(DM_mean = mean(DM))

## # A tibble: 7 × 2
##   Localisation DM_mean
##   <fct>          <dbl>
## 1 1               90.4
## 2 2               90.3
## 3 3               89.7
## 4 4               91.4
## 5 5               90.1
## 6 6               90.0
## 7 7               90.5

Calculer la médiane et l’écart-type pour chaque site de production.

Localisation	DM_mean	DM_q50	DM_sd
1	90.40	90.51	0.44
2	90.26	90.29	0.25
3	89.69	89.79	0.41
4	91.37	91.32	0.45
5	90.13	90.12	0.41
6	89.99	89.99	0.28
7	90.50	90.53	0.64

Modélisation statistique

On cherche à répondre à la question suivante : Les taux de matière sèche moyens à l’échelle de toute la production diffèrent-ils d’un site à l’autre ?

Mise en place de l’analyse statistique

Donner l’expression du modèle statistique M\(_1\) permettant de répondre à cette question ? Quels sont les paramètres de ce modèle ?
Quelles sont les hypothèses H\(_{0}\) et H\(_{1}\) du test de l’existence de différences moyennes de taux de matière sèche entre les sites de production ? Exprimer ces hypothèses à partir des paramètres du modèle de la question précédente.

Ajustement du modèle

A l’aide des fonctions lm et coef, donner la valeur estimée des paramètres du modèle d’analyse de la variance M\(_1\) introduit ci-dessus.
Donner l’expression mathématique du modèle nul M\(_0\).
Le paramètre désigné par le nom Intercept est-il estimé à la même valeur dans les modèles M\(_0\) et M\(_1\) ? Pourquoi ?

La qualité d’ajustement d’un modèle est mesurée par la somme des carrés des écarts entre les valeurs observées de la variable réponse et les valeurs ajustées par le modèle, que l’on nomme RSS (residual sum of squares).

Selon ce critère de qualité d’ajustement, peut-on dire que le modèle M\(_1\) est beaucoup mieux ajusté aux données que le modèle M\(_0\) ? Proposer une évaluation quantitative de ce gain d’ajustement.
Quelle est la valeur estimée de l’écart-type résiduel du modèle M\(_{1}\) ?

Test de l’effet site de production sur la quantité de matière sèche

Quelle est l’expression de la statistique de test permettant de tester l’existence de différences moyennes entre les lieux de production ? Quelle est la valeur prise par cette statistique de test ?
Quelle est la distribution \(\mathcal{F}_{0}\) sous l’hypothèse H\(_{0}\) de la statistique de test \(F\) introduite à la question précédente ?

Conclusion de l’étude

La fonction pf(q = .., df1 = .. , df2= .. , lower.tail = FALSE) donne la probabilité qu’une variable aléatoire suivant une loi de Fisher de paramètre df1, df2 dépasse la valeur q.

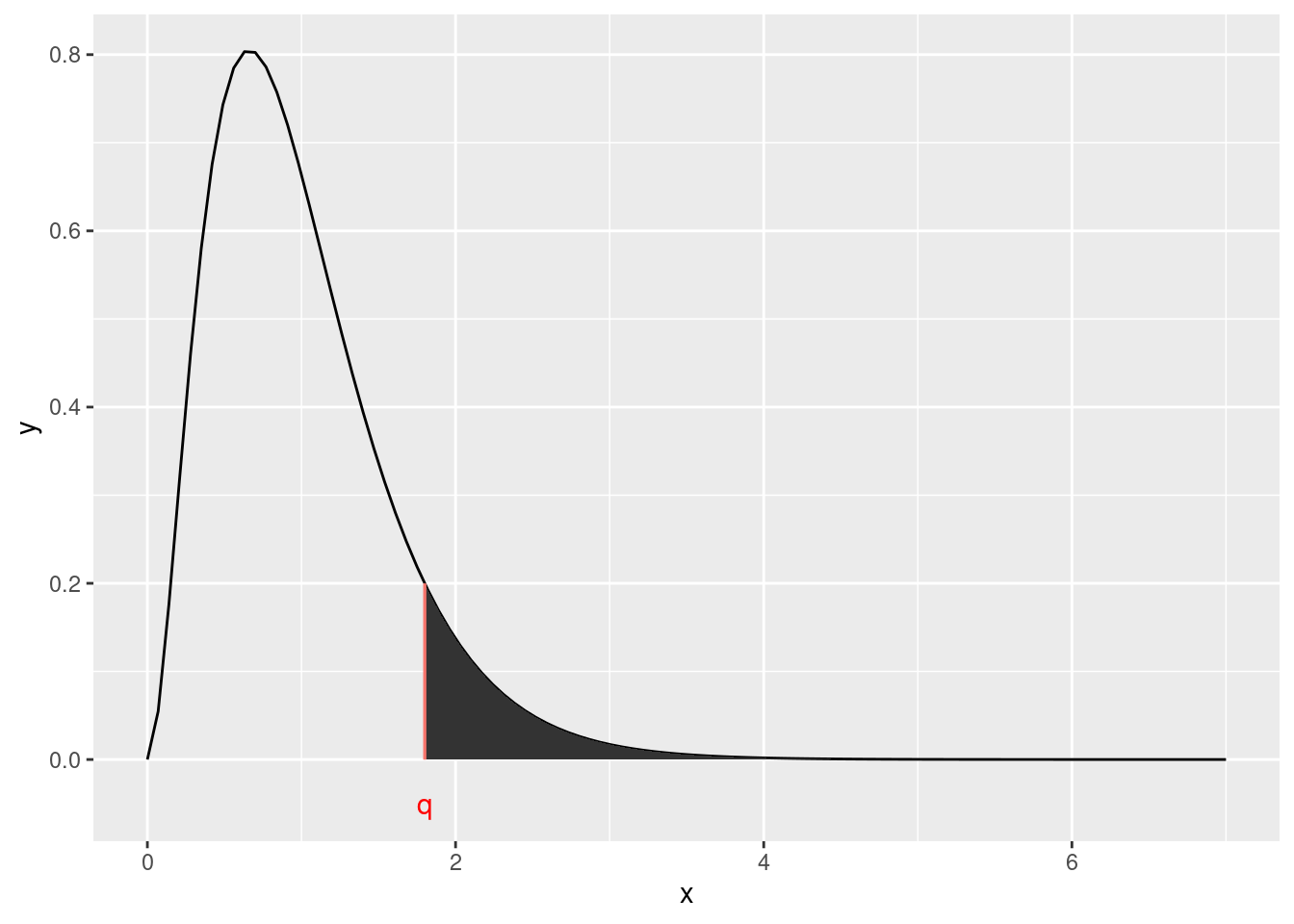
En déduire la p-value du test de comparaison des teneurs moyennes en matières sèches entre les sites de production.
En déduire une réponse à la question initialement posée.
Utiliser la fonction ‘anova’ pour repérer dans son résultat toutes les quantités que nous avons calculées dans ce TD.